Ламинарный поток воды

(от лат. lami­na – пла­стин­ка), те­че­ние жид­ко­сти или га­за, при ко­то­ром тра­ек­то­рии час­тиц сре­ды прак­ти­че­ски па­рал­лель­ны на­прав­ле­нию осн. по­то­ка. В об­щем слу­чае разл. слои жид­ко­сти или га­за дви­жут­ся с раз­ны­ми ско­ро­стя­ми, при­чём в Л. т. от­сут­ст­ву­ет пе­ре­ме­ши­ва­ние со­сед­них сло­ёв сре­ды. Л. т. на­блю­да­ет­ся в очень вяз­ких жид­ко­стях, а так­же при дос­та­точ­но мед­лен­ном об­те­ка­нии жид­ко­стью или га­зом тел ма­лых раз­ме­ров.

Л. т. на­блю­да­ют­ся в уз­ких (ка­пил­ляр­ных) труб­ках, в слое смаз­ки в под­шип­ни­ках, в тон­ком по­гра­нич­ном слое вбли­зи об­те­кае­мой по­верх­но­сти. Тео­рия Л. т. при­ме­ня­ет­ся при ре­ше­нии ря­да за­дач фи­зи­ки и хи­мич. тех­но­ло­гии, напр. при рас­смот­ре­нии те­че­ний в тон­ких плён­ках жид­ко­сти.

Представление об особенностях Л. т. даёт хорошо изученный случай движения в круглой цилиндрич. трубе. Для этого течения R е Кр

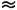
2200, где Re=

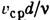
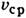
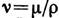
— кинематич. коэф. вязкости,

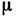
— динамич. коэф. вязкости,

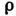
— плотность жидкости). Т. о., практически устойчивое Л. т. может иметь место или при сравнительно медленном течении достаточно вязкой жидкости или в очень тонких (капиллярных) трубках. Напр., для воды (

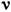
=10-6 м 2/с при 20° С) устойчивое Л. т. с

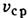
При Л. т. в неограниченно длинной трубе скорость в любом сечении трубы изменяется по закону

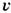
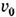
(1 — -r2/ а2), где а — радиус трубы, r — расстояние от оси,

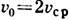
— осевая (численно максимальная) скорость течения; соответствующий параболич. профиль скоростей показан на рис. а. Напряжение трения изменяется вдоль радиуса по линейному закону

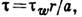
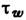
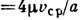
— напряжение трения на стенке трубы. Для преодоления сил вязкого трения в трубе при равномерном движении должен иметь место продольный перепад давления, выражаемый обычно равенством P1-P2

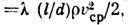
где p1 и р 2 — давления в к.-н. двух поперечных сечениях, находящихся на расстоянии l друг от друга,

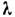
— коэф. сопротивления, зависящий от

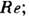
для Л. т.

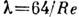
. Секундный расход жидкости в трубе при Л. т. определяет Пуазейля закон. В трубах конечной длины описанное Л. т. устанавливается не сразу и в начале трубы имеется т. н. входной участок, на к-ром профиль скоростей постепенно преобразуется в параболический. Приближённо длина входного участка

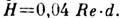
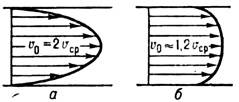
Распределение скоростей по сечению трубы: а — при ламинарном течении; б — при турбулентном течении.

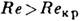
течение становится турбулентным, существенно изменяются структура потока, профиль скоростей (рис., 6 )и закон сопротивления, т. е. зависимость

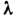
от Re (см. Гидродинамическое сопротивление).

Кроме труб Л. т. имеет место в слое смазки в подшипниках, вблизи поверхности тел, обтекаемых маловязкой жидкостью (см. Пограничный слой), при медленном обтекании тел малых размеров очень вязкой жидкостью (см., в частности, Стокса формула). Теория Л. т. применяется также в вискозиметрии, при изучении теплообмена в движущейся вязкой жидкости, при изучении движения капель и пузырьков в жидкой среде, при рассмотрении течений в тонких плёнках жидкости и при решении ряда др. задач физики и физ. химии.

Лит.: Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1954; Лойцянский Л. Г., Механика жидкости и газа, 6 изд., М., 1987; Тар г С. М., Основные задачи теории ламинарных течений, М.- Л., 1951; Слезкин Н. А., Динамика вязкой несжимаемой жидкости, М., 1955, гл. 4 — 11. С. М. Тарг.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
.

Примеры ламинарного течения в основном встречаются в тех случаях, когда течение канала сравнительно меньше, чем обычное течение. В этой статье приведены примеры ламинарного течения и связанных с ним вещей.

11+ примеров ламинарного потока перечислены ниже:

В чем смысл ламинарного течения?

В ламинарном потоке физические величины остаются неизменными, именно по этой причине ламинарный поток также называют потоком линии тока. В ламинарном потоке давление, скорость и многие другие физические величины остаются неизменными.

Ламинарное течение объясняют тем, что вязкая жидкость течет при движении, при котором молекулы вязкой жидкости могут двигаться параллельными слоями в определенный промежуток времени. В ламинарном течении скорость и давление и другие физические параметры остаются одинаковыми у каждой из частиц параллельных слоев.

Изображение – ламинарное течение;Кредит изображения — Википедия

Когда поток вязкой жидкости движется через замкнутую систему, такую ​​как стержень или трубу, и середину плоских пластин, возникает ламинарное течение. Ламинарное течение вязкой жидкости зависит от вязкость, скорость и форма или размер стержня.

От каких факторов зависит течение ламинара?

Если мы пройдем через закон Пуазейля тогда легко понять, как ламинарное течение зависит от физического фактора.

Компания течение ламинарного зависит от некоторых факторов. Факторы,

Вязкость

Ламинарный поток зависит от вязкости. отношения с поток ламинарный и вязкость косвенно пропорциональны друг другу. Означает, что если скорость вязкости увеличивается, то значение ламинарного потока уменьшается, а если скорость вязкости уменьшается, то значение ламинарного потока увеличивается.

Скорость

Ламинарный поток зависит от скорости. Отношения с поток ламинарный и скорость прямо пропорциональна. Это означает, что если скорость увеличивается, то значение ламинарного потока также увеличивается, а если скорость уменьшается, значение ламинарного потока также уменьшается.

Давление

Ламинарный поток зависит от давления. Отношения с поток ламинарный и давление прямо пропорциональны друг другу. Это означает, что если скорость давления увеличивается, то значение ламинарного потока также увеличивается, а если скорость давления уменьшается, то значение ламинарного потока также уменьшается таким же образом.

Размер стержня или трубы

Ламинарный поток зависит от размера стержня или трубы. Отношения с что собой представляет поток ламинарный и размер стержня или трубы косвенно пропорциональны друг другу. Означает, что если скорость размера стержня или трубы увеличивается, то значение ламинарного потока уменьшается, а если скорость размера стержня или трубы уменьшается, то значение ламинарного потока увеличивается.

Связь между числом Рейнольдса и потоком жидкости

Число Рейнольдса является безразмерным физическим фактором. По числу Рейнольдса легко можно оценить тип течения вязкой жидкости. Число Рейнольдса легко может понять нас поток ламинарный или турбулентный.

Связь между числом Рейнольдса и потоком жидкости приведена ниже:

Re = число Рейнольдса

ρ = плотность вязкой жидкости

V = характерная скорость вязкой жидкости

L = характерная длина для вязкой жидкости

μ = динамическая вязкость вязкой жидкости

v = кинематическая вязкость вязкой жидкости.

Изменение среднего состояния динамической вязкости и кинематической вязкости приведено ниже,

v = мк/р

Число Рейнольдса

Число Рейнольдса можно получить как отношение силы инерции к силе вязкости.

Математически число Рейнольдса можно записать как

Re = ρuL/μ

u = скорость потока вязкой жидкости

L = линейный размер характеристики вязкой жидкости

С помощью числа Рейнольдса мы можем оценить несколько свойств жидкости, такие как вязкость, скорость, длина, давление и многие другие.

Самолеты

Самолет — это машина или транспортное средство, которое может летать при поддержке воздуха. Самолет может летать, используя силу статической подъемной силы, силу динамической подъемной силы с аэродинамическим профилем. Самолет является примером ламинарного потока, который мы используем в нашей практической повседневной жизни. С помощью самолетов любой может добраться до нужного места за очень короткое время.

Изображение – Самолет;Кредит изображения — Unsplash

Каналы

Канал является примером ламинарного потока, который мы используем в нашей практической повседневной жизни. Канал на самом деле водный путь, который сделан искусственно для передачи транспортных средств в водный путь или для создания управления дренажной системой. Канал может проходить свободно, по ровной спокойной поверхности, где вода легко может течь под напором атмосферного воздуха.

Изображение – Канал;Кредит изображения — Wikimedia Commons

Ривер

Река является примером ламинарного течения, которое мы используем в нашей практической повседневной жизни. Река на самом деле является естественным водным путем, глубина которого может быть огромной или мелкой. В реке вода падает вниз по течению под действием силы тяжести. Река меньшего размера, также известная как ручей, ручей или ручей.

Изображение – Река;Кредит изображения — Wikimedia Commons

Отводы

Кран является примером ламинарного потока, который мы используем в нашей практической повседневной жизни. Когда вода поступает из крана, поток идет прямо, турбулентности нет. Когда вода поступает из-под крана, в этот момент давление и вязкость становятся одинаковыми в каждой точке воды.

Наливание чая из чайника

Наливание чая из чайника — пример ламинарного потока, который мы используем в нашей практической повседневной жизни. Когда чай поступает через сопло чайника, поток будет прямолинейным, и здесь нет турбулентности, поэтому возникает ламинарный поток. Когда чай выливается из чайника, в этот момент давление, вязкость и другие физические параметры остаются одинаковыми в каждой точке чая.

Изображение – Чай льется из чайника; Кредит изображения — Snappygoat

Вязкая жидкость

Любая вязкая жидкость является примером ламинарного течения, которое мы используем в нашей практической повседневной жизни. В каждой вязкой жидкости давление, вязкость и другие физические параметры остаются одинаковыми в каждой точке жидкости, поэтому возникает ламинарное течение.

Фонтаны

Фонтан является примером ламинарного потока, который мы используем в нашей практической повседневной жизни. Фонтан на самом деле является резервуаром, который используется в качестве украшения. В декоративный резервуар в основном сбрасывается вода. В каждом фонтане давление, вязкость и другие физические параметры остаются одинаковыми в каждой точке воды, поэтому возникает ламинарное течение.

Изображение – Фонтан;Кредит изображения — Wikimedia Commons

Курение

Дым является примером ламинарного потока, который мы создаем в нашей практической повседневной жизни. При появлении дыма турбулентность отсутствует, поэтому возникает ламинарное течение. В дыме давление, вязкость и другие физические параметры остаются одинаковыми в каждой точке.

Изображение – Дым свечи;Кредит изображения — Википедия общин

Водяной шар

Воздушный шар с водой является примером ламинарного потока, который мы используем в нашей практической повседневной жизни. Когда вода проходит через баллон, поток жидкости будет прямолинейным, и турбулентность отсутствует, поэтому возникает ламинарный поток.

Изображение – Водяной шар;Кредит изображения — Wikimedia Commons

Кровоток

Кровоток пример ламинарного потока, который мы используем в нашей практической повседневной жизни. Когда кровь течет, этот временной слой будет однонаправленным.

Изображение – кровоток;Кредит изображения — Википедия общин

Мед бежит из контейнера

Мед, вытекающий из контейнера, является примером ламинарного потока, и в это время турбулентность отсутствует, а вязкость и скорость остаются одинаковыми в каждой точке меда.

В этой статье будет обсуждаться термин «ламинарное течение в трубе» и ламинарное течение в трубе, связанные с несколькими фактами. Линейный поток — это еще один термин для ламинарного потока.

Ламинарный поток в трубе или линию потока в трубе можно описать таким образом, когда жидкость течет внутри трубы или трубы в движении, в то время как между слоями нет разрыва. При малой скорости жидкость может течь очень плавно без поперечного перемешивания.

Что такое ламинарное течение в трубе?

Ламинарное течение в трубе может характеризоваться высокоупорядоченным движением и плавной обтекаемостью. Ламинарный поток жидкости в трубопроводе протекает равномерно как по направлению, так и по скорости.

Ламинарный поток в трубе может быть получен как,

• Если диапазон числа Рейнольдса составляет от 2000 до менее 2000, то такое течение жидкости называется ламинарным течением.
• Математический анализ ламинарного течения не сложен.
• Скорость ламинарного потока очень мала, поэтому поток жидкости очень плавный, без поперечного перемешивания.
• Регулярное движение можно наблюдать в жидкостях, которые ламинарно текут и текут в движении.
• Ламинарное течение в общем редком типе течения жидкости.
• Среднее движение позволяет наблюдать, в какую сторону течет жидкость.
• В ламинарном потоке профиль скорости очень меньше в центральной части трубы.
• При ламинарном течении профиль скорости находится высоко у стенки трубы.

Изображение — В случае движущейся пластины в жидкости обнаружено, что существует слой (пластина), который движется вместе с пластиной, и слой неподвижной жидкости рядом с любой неподвижной пластиной;Кредит изображения — Википедия

Формула ламинарного течения в трубе

С помощью уравнения Пуазейля мы можем понять падение давления потока жидкости произошло для вязкости. Уравнение Гегена Пуазейля применимо для ньютоновской жидкости и несжимаемой жидкости.

Уравнение Гегена Пуазейля неприменимо для близкого входа в трубу. Уравнение ламинарного потока:

Δp = величина разности давлений, возникающая в двух конечных точках трубы.

μ = динамическая вязкость жидкости, протекающей по трубе

L = длина трубы

Q = объемный расход

R = радиус трубы

A = площадь поперечного сечения трубы

Приведенное выше уравнение не подходит для очень короткой или очень длинной трубы, а также для жидкости с низкой вязкостью. В очень короткой или очень длинной трубе, а также для жидкости с низкой вязкостью возникает турбулентный поток, для которого уравнение Гегена Пуазейля неприменимо. В этом случае мы применили более полезное уравнение для расчета, такое как уравнение Дарси – Вейсбаха.

Отношение длины к радиусу трубы больше одной сорок восьмой числа Рейнольдса, что соответствует закону Гегена Пуазейля. Когда трубка очень короткая, в это время закон Гегена Пуазейля может привести к тому, что высокая скорость потока нефизична.

Течение жидкости ограничено по принципу Бернулли при исключающем ограничительном условии именно потому, что давление в потоке несжимаемой жидкости не может быть меньше нуля.

Δ р = 1/2ρ v-2

∆ p = 1/2ρ(QМакс/ π р2}2)

Ламинарный поток в выводе трубы

• Градиент давления
• Радиус узкой трубки
• Вязкость
• Длина трубки стрелы
• Сопротивление

Градиент давления (Delta P)

Перепад давления между двумя концами трубы определяется тем фактом, что каждая жидкость всегда будет течь из области высокого давления в область низкого давления.

Скорость потока рассчитывается по

Δ Р = Р1 — П2

Радиус узкой трубки

Поток жидкости напрямую изменяется с радиусом в степени четыре.

Вязкость (η)

Скорость потока жидкости обратно пропорциональна вязкости жидкости.

Длина трубки стрелы (L)

Скорость потока жидкости обратно пропорциональна длине узкой трубки.

Сопротивление (р)

Сопротивление рассчитывается как 8Ln/πr4 и, следовательно, закон Пуазейля

Q = (Δ P) R

Теплопередача в потоке трубы

Уравнение конвекции-диффузии тепловой энергии приведено ниже,

Уравнение левой части рассматривается конвективный теплообмен, которые переносятся движением жидкости. Радиальная скорость равна нулю, поэтому можно избежать уравнения первого члена в левой части.

Правая часть уравнения представляет тепловую диффузию. Поскольку поток является ламинарным, мы можем предположить, что безразмерное число Эккерта, которое представляет собой отношение между кинетической энергией потока и его движущей силой теплопередачи, достаточно мало, чтобы можно было пренебречь вязкой диссипацией.

Поэтому уравнение тепловой энергии можно дополнить профилем скорости, определенным в предыдущем разделе.

Условие постоянного значения теплового потока подразумевает, что разница температур между стенкой и жидкостью одинакова. Однако мы уже знаем, что температура жидкости внутри трубы непостоянна. Поэтому введем объемную среднюю температуру, обозначаемую как:

Предполагая, что локальный градиент температуры и градиент средней температуры в объеме в продольном направлении равны и имеют постоянную величину, интегрирование вышеупомянутого уравнения переноса тепловой энергии приводит к следующей формуле для радиального распределения температуры:

Где a = k/ρc – тепловая коэффициент диффузии . Градиент средней температуры можно получить, применив желаемый объемный расход Q и тепловой поток q к уравнению сохранения тепла:

Qρc dTm/dz = πDq

Чтобы удовлетворить условию постоянного потока на стенке, значение температуры стенки было связано с градиентом средней температуры в объеме.

Ламинарное течение в граничных условиях трубы

Ламинарные пограничные слои возникают, когда движущаяся вязкая жидкость соприкасается с поверхностью, находящейся в твердом состоянии, и пограничный слой, слой вращающейся жидкости формируется в ответ на действие условия прилипания границы и вязкости поверхности.

Число Рейнольдса для ламинарного течения в трубе

Значения ламинарного течения для конкретного определения числа Рейнольдса зависят от характера течения жидкости через трубу и геометрии системы, по которой течет жидкость.

Выражение для числа Рейнольдса для ламинарного течения в трубе приведено ниже:

Re = ρuDH/μ = и DH/ν = КТH/νА

Ре = Число Рейнольдса

ρ = плотность жидкости в трубе в килограммах на кубический метр.

u = средняя скорость потока жидкости в трубе, единица измерения – метр в секунду.

μ = динамическая вязкость жидкости, протекающей по трубе, в килограммах на метр в секунду.

A = площадь поперечного сечения трубы и блока в квадратных метрах

Q= объемный расход а единица кубический метр в секунду

DH = Гидравлический диаметр трубы, по которой течет жидкость, и единицей измерения является метр.

ν = кинематическая вязкость жидкости, протекающей по трубе, в единицах квадратный метр в секунду.

п = м/р

Изображение – сфера в потоке Стокса при очень низком числе Рейнольдса. Объект, движущийся через жидкость, испытывает силу сопротивления в направлении, противоположном его движению;Кредит изображения — Википедия

Число Нуссельта для ламинарного течения в трубе

Когда в этом случае внутренний ламинарный поток полностью развит, число Нуссельта для ламинарного течения в трубе может быть выражено как

Nu = хDh/kf

Nu = Число Нуссельта

h = коэффициент конвективной теплопередачи

kf = Теплопроводность жидкости, протекающей по трубе

Коэффициент трения при ламинарном течении в трубе

Коэффициент трения для ламинарного потока можно выразить как

fD = 64/Re

fD = Коэффициент трения

ρ = плотность жидкости в трубе и единица измерения в килограммах на кубический метр.

v = средняя скорость потока, единица измерения — метры в секунду.

D = диаметр трубы, по которой течет жидкость, единица измерения – метр.

Полностью развитое ламинарное течение в трубе

Полностью развитое течение возникает, когда вязкостные эффекты возникают из-за напряжения сдвига частицами жидкости, а стенка трубы создает полностью развитый профиль скорости.

Для этого жидкость должна пройти по длине прямой трубки. Скорость жидкости при полностью развитом потоке будет максимальной на центральной линии трубы (ламинарный поток по уравнению 1).

Скорость жидкости у стенок трубы теоретически будет равна нулю.

Скорость жидкости может быть выражена как средняя скорость.

Это уравнение применимо только к ламинарному потоку.

Ламинарное течение в круглой трубе

В круглой трубе, из которой жидкость течет ламинарно, диаметр выражается как D_c, для этого случая коэффициент трения потока обратно пропорциональна числу Рейнольдса, с помощью которого мы можем легко опубликовать или измерить физический параметр.

С помощью уравнения Дарси – Вейсбаха ламинарный поток в круглой трубе можно выразить как

Δp/L = 128/π = µQ/D4c

L = длина трубы, по которой течет жидкость

μ = динамическая вязкость текущей жидкости в трубе

Q = Объемный расход протекающей жидкости в трубе

Вместо средней скорости можно использовать объемный расход жидкости в трубе, выражение которого приведено ниже:

Dc = Диаметр трубы, по которой течет жидкость

Ламинарное течение в цилиндрической трубе

Цилиндрическая труба, в которой течет полный, равномерный диаметр, выраженный как D, потеря давления из-за вязких эффектов, выраженная как Delta p, прямо пропорциональна длине.

Ламинарное течение в цилиндрической трубе можно получить с помощью уравнения Дарси – Вейсбаха, приведенного ниже,

fD = Коэффициент трения Дарси

Ламинарное течение в профиле скорости трубы

Ламинарное течение возникает при очень малых скоростях, ниже порога в этой точке течение жидкости становится турбулентным.

Профиль скорости трубы для ламинарного потока можно определить с помощью числа Рейнольдса. Профиль скорости трубы при ламинарном течении также зависит от плотности и вязкости протекающей жидкости и размеров канала.

Q = объемный расход, единицей измерения является кубический метр в секунду.

Ламинарный поток в вертикальной трубе

Ниже показано ламинарное течение жидкости в вертикальной трубе.

Изображение. Профиль скорости, связанный с ламинарным потоком, напоминает колоду карт. Этот профиль течения жидкости в трубе показывает, что жидкость действует слоями, которые скользят друг по другу;Кредит изображения — Википедия

Ламинарное течение в шероховатой трубе

Компания падение давления в полностью развитом ламинарном потоке через трубу пропорциональна средней скорости или средней скорости в трубе. В ламинарном потоке коэффициент трения не зависит от шероховатости, поскольку пограничный слой покрывает шероховатость.

Большая советская энциклопедия. — М.: Советская энциклопедия.
.

Смотреть что такое «Ламинарное течение» в других словарях

Движение жидкости, наблюдаемое при малых скоростях, при котором отдельные струйки жидкости движутся параллельно друг другу и оси потока, называют ламинарный режим движения жидкости.

В этой статье подробно описывается процесс ламинарного режима, переход в ламинарного режима из турбулентный, формула и закон этого режима и многое другое.

Очень наглядное представление о ламинарном режиме движения жидкости можно получить из опыта Рейнольдса. Подробное описание здесь.

Ламинарное течение (от латинского lamina — пластинка, полоска) — вязкой жидкости течение, в котором частицы среды движутся упорядоченно по слоям и процессы переноса массы, импульса и энергии между слоями происходят на молекулярном уровне. Типичным примером Л. т. является обширный класс слоистых течений, в которых все частицы жидкости или газа имеют одно и то же направление движения. Наиболее подробно изучено Л. т. несжимаемой жидкости в трубках неограниченной длины и малого диаметра (впервые экспериментально этот случай изучался нем, учёным Г. Гагеном в 1839 и французским учёным Ж. Пуазёйлем в 1840). В этом случае каждая частица жидкости движется по прямолинейным траекториям, а зависимость скорости v частиц от расстояния r от оси трубы описывается параболическим законом:

v = vмакс(1-r2/а2),
где а — радиус трубы, vмакс — скорость на её оси.
При обтекании тел или при движении жидкости в каналах и трубах Л. т. имеет место лишь при Рейнольдса числах, меньших критического Re* (для описанного выше случая Re*(≈)2200). При Re(≥)Re* Л. т. становится неустойчивым и переходит в турбулентное течение. Л. т. реализуется, например, при движении летательного аппарата на достаточно больших высотах, а с уменьшением высоты полёта область существования Л. т. ограничена некоторой окрестностью передних кромок крыла, оперения, носовой части фюзеляжа и других элементов летательного аппарата.
В общем случае основой для теоретического анализа Л. т. служат Навье — Стокса уравнения. В некоторых частных случаях эти уравнения упрощаются, что позволяет получить аналитические решения задачи. Если движение среды происходит при достаточно больших Re, то Л. т. исследуется с помощью уравнений Л. Прандтля (см. Пограничный слой).
Авиация: Энциклопедия. — М.: Большая Российская Энциклопедия.
.
.

Жидкая среда вытекает из бака через прозрачную трубу и через кран уходит на слив. Таким образом жидкость течет с определенным небольшим и постоянным расходом.

На входе в трубу установлена тонкая трубочка по которой в центральную часть потока поступает подкрашенная среда.

При попадании краски в поток жидкости движущейся с небольшой скоростью красная краска будет двигаться ровной струйкой. Из этого опыта можно сделать вывод о слоистом течении жидкости, без перемешивания и вихреообразования.

Такой режим течения жидкости принято назыать ламинарным.

Рассмотрим основные закономерности ламинарного режима при равномерном движении в круглых трубах, ограничиваясь случаями, когда ось трубы горизонтальна.

При этом мы будем рассматривать уже сформировавшийся поток, т.е. поток на участке, начало которого находится от входного сечения трубы на расстоянии, обеспечивающем окончательный устойчивый вид распределения скоростей по сечению потока.

Имея ввиду, что ламинарный режим течения имеет слоистый(струйный) характер и происходит без перемешивания частиц, следует считать, что в ламинарном потоке будут иметь место только скорости, параллельные оси трубы, поперечные же скорости будут отсутствовать.

Можно представить себе, что в этом случае движущаяся жидкость как бы разделяется на бесконечно большое число бесконечно тонких цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися в направлении от стенок к оси трубы.

При этом скорость в слое, непосредственно соприкасающемся со стенками из-за эффекта прилипания равна нулю и достигает максимального значения в слое, движущемся по оси трубы.

Формула ламинарного режима течения

Принятая схема движения и введенные выше предположения позволяют теоретическим путем установить закон распределения скоростей в поперечном сечении потока при ламинарном режиме.

Для этого сделаем следующее. Обозначим внутренний радиус трубы через r и выберем начало координат в центре её поперечного сечения O, направив ось х по оси трубы, а ось z по вертикали.

Теперь выделим внутри трубы объем жидкости в виде цилиндра некоторого радиуса y длиной L и применим к нему уравнение Бернулли. Так как в следствии горизонтальности оси трубы z1=z2=0,
то

τ – единичная сила трения = — μ * dυ/dy

Подставляя значения R и τ в исходное уравнение получим

Задавая различные значения координаты y, можно вычислить скорости в любой точке сечения. Максимальная скорость, очевидно, будет при y=0, т.е. на оси трубы.

Для того, чтобы изобразить это уравнения графически, необходимо отложить в определенном масштабе от некоторой произвольной прямой АА скорости в виде отрезков, направленных по течению жидкости, и концы отрезков соединить плавной кривой.

Полученная кривая и представит собой кривую распределения скоростей в поперечном сечении потока.

График изменения силы трения τ по сечению выглядит совсем по другому. Таким образом, при ламинарном режиме в цилиндрической трубе скорости в поперечном сечении потока изменяются по параболическому закону, а касательные напряжения – по линейному.

Полученные результаты справедливы для участков труб с вполне развитым ламинарным течением. В действительности, жидкость, которая поступает в трубу, должна пройти от входного сечения определенный участок, прежде чем в трубе установится соответствующий ламинарному режиму параболический закон распределения скоростей.

Развитие ламинарного режима в трубе

Развитие ламинарного режима в трубе можно представить себе следующим образом. Пусть, например, жидкость входит в трубу из резервуара большого размеры, кромки входного отверстия которого хорошо закруглены.

В этом случае скорости во всех точках входного поперечного сечения будут практически одинаковы, за исключением очень тонкого, так называемого пристенного слоя(слоя вблизи стенок), в котором вследствие прилипания жидкости к стенкам происходит почти внезапное падение скорости до нуля. Поэтому кривая скоростей во входном сечении может быть представлена достаточно точно в виде отрезка прямой.

По мере удаления от входа, вследствие трения у стенок, слои жидкости, соседние с пограничным слоем, начинают затормаживаться, толщина этого слоя постепенно увеличивается, а движение в нем, наоборот, замедляется.

Центральная же часть потока (ядро течения), еще не захваченная трением, продолжает двигаться как одно целое, с примерно одинаковой для всех слоев скоростью, причем замедление движения в пристенном слое неизбежно вызывает увеличение скорости в ядре.

Таким образом, в середине трубы, в ядре, скорость течения все время возрастает, а у стенок, в растущем пограничном слое, уменьшается. Это происходит до тех пор, пока пограничный слой не захватит всего сечения потока и ядро не будет сведено к нулю. На этом формирование потока заканчивается, и кривая скоростей принимает обычную для ламинарного режима параболическую форму.

Переход от ламинарного течения к турбулентному

Ламинарное течения жидкости при некоторых условиях способно перейти в турбулентное. При повышении скорости течения потока слоистая структура потока начинает разрушаться, появляются волны и вихри, распространение которых в потоке говорит о нарастающем возмущении.

Постепенно количество вихрей начинает возрастать, и возрастает пока струйка не разобьется на множество перемешивающихся между собой более мелких струек.

Хаотичное движение таких мелких струек позволяет говорить о начале перехода ламинарного режима течения в турбулентное. С увеличением скорости ламинарное течение теряет свою устойчивость, при этом любые случайные небольшие возмущения, которые раньше вызывали только лишь малые колебания, начинают быстро развиваться.

Видео о ламинарном течении

В бытовом случае переход одного режима течения в другой можно отследить на примере струи дыма. Сначала частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым практически неподвижен. Со временем в некоторых местах вдруг возникают крупные вихри, которые двигаются по хаотичным траекториям. Эти вихри распадаются на более маленькие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом.